1. 2.2 Derivative Graphically And Numericallyap Calculus Algebra
2. 2.2 Derivative Graphically And Numericallyap Calculus Solver
3. 2.2 Derivative Graphically And Numericallyap Calculus Formulas
4. 2.2 Derivative Graphically And Numericallyap Calculus Calculator

3: For 16, graph the derivative of the given functions Deborah Hughes-Hallett Patti Frazer Lock Andrew M. 920 Calculus Applied Calculus 5 Edition. 1 Lecture 2.2: Techniques of Differentiation (Finding Derivatives of Functions Easily).

GRAPHING OF FUNCTIONS USING FIRST AND SECOND DERIVATIVES

The following problems illustrate detailed graphing of functions of one variable using the first and second derivatives. Problems range in difficulty from average to challenging. If you are going to try these problems before looking at the solutions, you can avoid common mistakes by carefully labeling critical points, intercepts, and inflection points. In addition, it is important to label the distinct sign charts for the first and second derivatives in order to avoid unnecessary confusion of the following well-known facts and definitions.

Here are instruction for establishing sign charts (number line) for the first and second derivatives. To establish a sign chart (number lines) for f' , first set f' equal to zero and then solve for x . Mark these x-values underneath the sign chart, and write a zero above each of these x-values on the sign chart. In addition, mark x-values where the derivative does not exist (is not defined). For example, mark those x-values where division by zero occurs in f' . Above these x-values and the sign chart draw a dotted vertical line to indicate that the value of f' does not exist at this point. These designated x-values establish intervals along the sign chart. Next, pick points between these designated x-values and substitute them into the equation for f' to determine the sign ( + or - ) for each of these intervals. Beneath each designated x-value, write the corresponding y-value which is found by using the original equation y = f(x) . These ordered pairs (x, y) will be a starting point for the graph of f . This completes the sign chart for f' . Establish a sign chart (number line) for f' in the exact same manner. To avoid overlooking zeroes in the denominators of f' and f' , it is helpful to rewrite all negative exponents as positive exponents and then carefully manipulate and simplify the resulting fractions.

FACTS and DEFINITIONS

1. If the first derivative f' is positive (+) , then the function f is increasing ().

2. If the first derivative f' is negative (-) , then the function f is decreasing ().

3. If the second derivative f' is positive (+) , then the function f is concave up ().

4. If the second derivative f' is negative (-) , then the function f is concave down ().

5. The point x=a determines a relative maximum for function f if f is continuous at x=a , and the first derivative f' is positive (+) for x<a and negative (-) for x>a . The point x=a determines an absolute maximum for function f if it corresponds to the largest y-value in the range of f .

6. The point x=a determines a relative minimum for function f if f is continuous at x=a , and the first derivative f' is negative (-) for x<a and positive (+) for x>a . The point x=a determines an absolute minimum for function f if it corresponds to the smallest y-value in the range of f .

7. The point x=a determines an inflection point for function f if f is continuous at x=a , and the second derivative f' is negative (-) for x<a and positive (+) for x>a , or if f' is positive (+) for x<a and negative (-) for x>a .

8. THE SECOND DERIVATIVE TEST FOR EXTREMA (This can be used in place of statements 5. and 6.) : Assume that y=f(x) is a twice-differentiable function with f'(c)=0 .

a.) If f'(c)<0 then f has a relative maximum value at x=c .

b.) If f'(c)>0 then f has a relative minimum value at x=c .

These are the directions for problems 1 through 10. For each function state the domain. Determine all relative and absolute maximum and minimum values and inflection points. State clearly the intervals on which the function is increasing (), decreasing (), concave up (), and concave down (). Determine x- and y-intercepts and vertical and horizontal asymptotes when appropriate. Neatly sketch the graph.

• PROBLEM 1 : Do detailed graphing for f(x) = x³ - 3x² .

  Click HERE to see a detailed solution to problem 1.
  

• PROBLEM 2 : Do detailed graphing for f(x) = x⁴ - 4x³ .

  Click HERE to see a detailed solution to problem 2.
  

• PROBLEM 3 : Do detailed graphing for f(x) = x³ (x-2)² .

  Click HERE to see a detailed solution to problem 3.
  

• PROBLEM 4 : Do detailed graphing for .

  Click HERE to see a detailed solution to problem 4.
  

• PROBLEM 5 : Do detailed graphing for .

  Click HERE to see a detailed solution to problem 5.
  

• PROBLEM 6 : Do detailed graphing for .

  Click HERE to see a detailed solution to problem 6.
  

• PROBLEM 7 : Do detailed graphing for f(x) = x - 3x^1/3 .

  Click HERE to see a detailed solution to problem 7.
  

• PROBLEM 8 : Do detailed graphing for .

  Click HERE to see a detailed solution to problem 8.
  

• PROBLEM 9 : Do detailed graphing for for x in .

  Click HERE to see a detailed solution to problem 9.
  

• PROBLEM 10 : Do detailed graphing for .

  Click HERE to see a detailed solution to problem 10.
  

• PROBLEM 11 : Consider the cubic polynomial y = A x³ + 6x² - Bx , where A and B are unknown constants. If possible, determine the values of A and B so that the graph of y has a maximum value at x= -1 and an inflection point at x=1 .

  Click HERE to see a detailed solution to problem 11.

Click HERE to return to the original list of various types of calculus problems.

Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by clicking on the following address :

Duane Kouba
1998-06-03

So you may have memorized all of the derivative rules. You might be able to derive f '(x) from f(x) no matter how complicated the function is. But how are you at estimating derivatives directly from the graph?

As we’ll see in this review article, it’s all about slope!

The Derivative Measures Slope

Let’s begin with the fundamental connection between derivatives and graphs of functions.

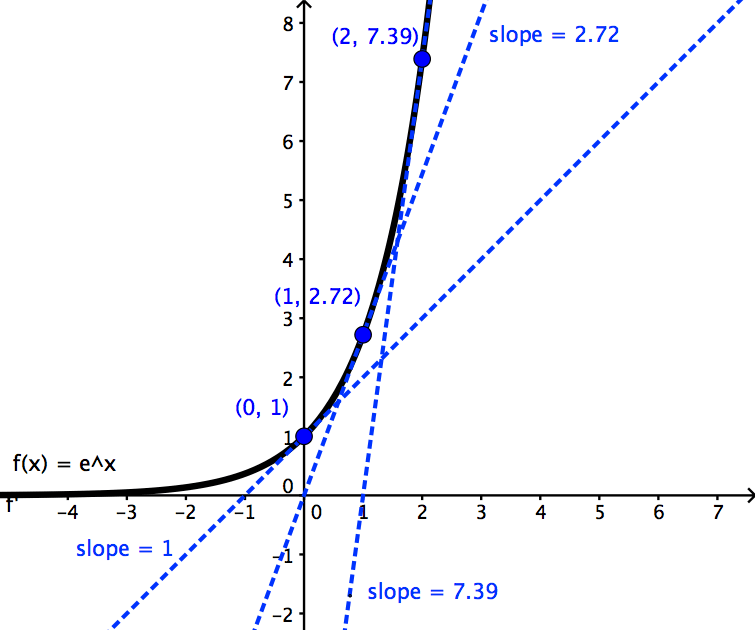
The derivative value f '(a) equals the slope of the tangent line to the graph of y = f(x) at x = a.

I recommend brushing up on the idea of tangent lines first. Here are a few resources that might help.

Example — Estimating Derivatives using Tangent Lines

Use the information in the graph of f(x) below to estimate the value of f '(1).

Graph of a parabola with a tangent line attached at (1, 1).

Solution

Remember, derivative values are slopes! So f '(1) is equal to the slope of the tangent line attached to the graph at x = 1.

All it takes is two points on a line to determine slope. One point is easy to spot because it’s also on the graph of f itself: (1, 1). Next we look along the tangent line until we find another point whose coordinates are easy to estimate. Try to find a point that crosses an “intersection,” because then it will have integer coordinates. For example, (2, 3), or (3, 5), or (0, -1), etc.

I’m going to pick (3, 5) as my second point. However, if you pick any other point, as long as it’s on the tangent line, then your answer should be equal (or very close) to mine.

Next, use the slope formula (RISE over RUN) to compute the slope of the tangent line.

Therefore f '(1) = 2.

Increasing, Decreasing, and Turning Around

Ok, so the first example may have been pretty easy. How hard can it get?

Sometimes we have to estimate all of the derivative values! In other words, given the graph of a function f(x), it should be possible to sketch a graph of f '(x).

There are three things to keep in mind for differentiable functions.

• If f is increasing on an interval, then f ' > 0 (above the x-axis) in that interval.
• If f is decreasing on an interval, then f ' < 0 (below the x-axis) in that interval.
• If f turns around smoothly at a point x = a, then f '(a) = 0 (intersecting the x-axis).

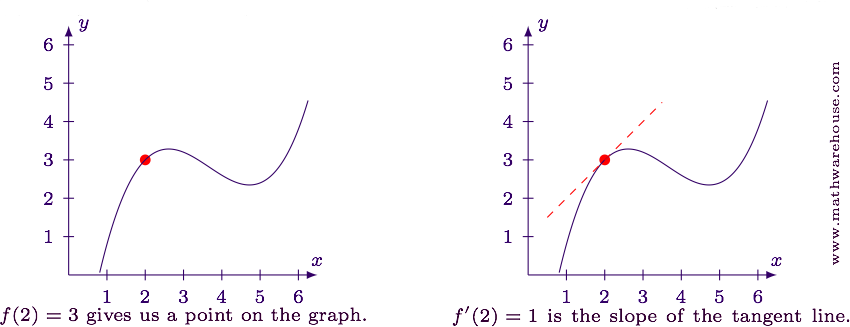
Example — Estimating the Graph of a Derivative

Sketch the graph of the derivative of the function whose graph is shown below.

Solution

First identify the two turnaround points: at x = -2 and 0. This means that f '(-2) = f '(0) = 0.

Then, identify the intervals on which the graph increases and decreases. When f is increasing, we have f ' > 0. When f is decreasing, we have f ' < 0.

The graph of a function gives information about its derivative… if you know how to analyze it.

The graph below shows the original in black and a sketch of its derivative in blue.

Notice how the blue curve fits the description of f '.

• The blue curve is above the x-axis whenever f increases.
• The blue curve is below the x-axis whenever f decreases.
• The blue curve crosses the x-axis whenever f has a turnaround point.

Non-Differentiable Points

The methods for estimating derivatives so far have ignored an essential issue. What happens when the function fails to have a derivative value at a given point?

Any point x = a at which f '(a) does not exist is called a point of non-differentiability.

If a is such a point, then there will either be a hole or break in the graph of f ' at x = a.

Three things could cause such behavior.

1. The original function is undefined or discontinuous.
2. There is a corner point in the original function’s graph.
3. The tangent line is vertical.

2.2 Derivative Graphically And Numericallyap Calculus Algebra

Let’s explore the three situations in the following example.

Example — Estimating Derivatives With Non-Differentiable Points

Sketch the graph of the derivative of the following function.

Solution

There is a lot going on in this graph!

• There’s a vertical asymptote at x = -5. Because f is undefined at this point, we know that the derivative value f '(-5) does not exist.
• The graph comes to a sharp corner at x = 5. Derivatives do not exist at corner points.
• There is a cusp at x = 8. The derivative value becomes infinite at a cusp.

Aside from these important landmarks, there’s also one turnaround point, at x = 0. Let’s analyze what happens in the intervals between the special points.

But what exactly happens near x = -5, 5, and 8?

At x = -5, the original graph follows a vertical asymptote. By definition, the function values are approaching ∞ or -∞ the closer x gets to -5. As a result, the function gets infinitely steep as x → -5. Infinite steepness means infinite slope values, so f ' must also have a vertical asymptote at x = -5.

Next, the corner point at x = 5 represents a very sudden change in direction. Rather than turning around smoothly, the function instantly changes course. That means that there will be a jump in the derivative value when crossing x = 5.

(For more about jump discontinuities and related topics, check out: AP Calculus Review: Discontinuities.)

Finally, there is a cusp at x = 8. At a cusp, the graph’s tangent line becomes so steep that it’s effectively vertical. That means that the slope is infinite, and again there will be a vertical asymptote in the graph of f '.

Let’s put it all together now. The blue graph represents just a sketch of the derivative curve (not 100% accurate, but close enough for our purposes).

Notice not only the odd behavior near each point of discontinuity, but also how the derivative values are above the x-axis when f is increasing and below the axis when f is decreasing.

Sketch of the derivative of a complicated function. Original in black; derivative in blue.

Conclusion

It’s important to know how to identify the derivative of a function based only on its graph. Fortunately, the AP Calculus exams will not require you to sketch the derivative curve itself, but may ask you to pick which answer choice best matches it.

Use smooth turnaround points as landmarks. Make sure you understand the strange behavior at non-differentiable points. And fill in the details by analyzing where f increases and decreases.

2.2 Derivative Graphically And Numericallyap Calculus Solver

About Shaun Ault

Shaun earned his Ph. D. in mathematics from The Ohio State University in 2008 (Go Bucks!!). He received his BA in Mathematics with a minor in computer science from Oberlin College in 2002. In addition, Shaun earned a B. Mus. from the Oberlin Conservatory in the same year, with a major in music composition. Shaun still loves music -- almost as much as math! -- and he (thinks he) can play piano, guitar, and bass. Shaun has taught and tutored students in mathematics for about a decade, and hopes his experience can help you to succeed!

2.2 Derivative Graphically And Numericallyap Calculus Formulas

2.2 Derivative Graphically And Numericallyap Calculus Calculator

Magoosh blog comment policy: To create the best experience for our readers, we will approve and respond to comments that are relevant to the article, general enough to be helpful to other students, concise, and well-written! :) If your comment was not approved, it likely did not adhere to these guidelines. If you are a Premium Magoosh student and would like more personalized service, you can use the Help tab on the Magoosh dashboard. Thanks!